Istina o šahovskom rejtingu

Оригинални чланак "Истина о шаховском рејтингу" Др Андрејић Владице можете преузети у ПДФ формату.

Vladica Andrejić

Univerzitet u Beogradu, Matematički fakultet, Srbija

Osnovni problem šahovskog rejting sistema je odrediti funkciju f, koja razlici u rejtingu dodeljuje verovatnoću, odnosno očekivani rezultat. To zapravo znači da ukoliko igrač A sa rejtingom Ra odigra N partija protiv igrača B sa rejtingom Rb, možemo očekivati da će A sakupiti N*f(Ra-Rb) poena, odnosno da će konačni odnos poena u meču A protiv B biti f(Ra-Rb):f(Rb-Ra), pri čemu je naravno f(Rb-Ra)=1-f(Ra-Rb).

Ponašanje rejtinga zavisi od funkcije f , a njene osobine možemo potražiti u najjednostavnijem slučaju kada tri igrača A, B i C, između sebe odigraju ogroman broj partija. Ako znamo rezultat A protiv B i rezultat B protiv C, možemo li naslutiti rezultat A protiv C?

Jedna od mogućih hipoteza je da je priroda rejtinga takva da čuva odgovarajuće odnose. To zapravo znači da ukoliko A i B igraju u odnosu a:b, a B i C u odnosu b:c, tada očekujemo da A i C igraju u odnosu a:c. Ako sa x i y označimo razliku u rejtingu igrača A i B, odnosno B i C, tada se hipoteza može zapisati u vidu funkcionalne jednačine

koja važi za svako realno x i y. Pojednostavljenje jednačine (1) sa x=y dovodi do formule

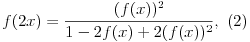koja se lakše može primeniti, a nije teško dokazati da rešenje ovih jadnačina, predstavlja familiju funkcija oblika

gde je C neka konstanta. Sam izbor konstante C je nevažan jer on samo normira jedinicu mere rejtinga, te tako jednom rejting poenu odgovara verovatnoća od f(1)=1/(1+C).

jako dobro oponaša prave (FIDE) vrednosti za f [2], ali da se ipak u računima koriste direktno odgovarajuće tablice [1]. Na osnovu (4) mogli bi reći da je C izabrano tako da važi f(400)=10/11, ali utisak kvari to što je 10/11 ~ 0.91, dok u tablicama stoji vrednost 0.92. Kompletne FIDE tablice napravljene su na osnovu drugačije distribucije, ali odstupanja su jako mala i iznose oko 1% (u oba smera).

Da li zakon o očuvanju odnosa iz naše hipoteze zaista dobro opisuje realnost? Ja sam prvi put posumnjao u njega kada sam pročitao Sonas-ov članak [3] u kome se kao alternativa predlaže linearna skala. Zbog toga sam izvršio nekoliko eksperimenata koristeći podatke sa mog vebsajta Večiti Šah [4], koji je od početka 2006. ispratio skoro sve turnire (klasični tempo, vikendi, cugeri) koji vrede, a igrani su na području Srbije i Crne Gore.

U Prvom eksperimentu posmatrao sam sve rezultate partija na klasičnom tempu igre, igranih u Srbiji i Crnoj Gori, gde su oba igrača imala FIDE rejting. Program je razvrstavao partije u klase od po 10 rejting poena, odnosno uzimao je zaokruženi broj razlike u rejtingu podeljenu sa 10 i vršio statističku obradu. Veoma interesantan rezultat je da su svi dobijeni procenti strogo manji od projektovanih (formule (3) i (4)), barem za prvih 50 klasa, odnosno do razlike od 500 rejting poena, dok je za veće razlike uzorak premali za ozbiljno tumačenje. Objašnjenje ovog fenomena možda treba tražiti u, po meni nepouzdano, računanje FIDE rejtinga, pogotovo na nižim rejtinzima (ogromna većina igrača iz ovog eksperimenta imaju rejting ispod 2400), jer je identičan eksperiment, ovoga puta na svetskim superturnirima dao prilično zadovoljavajuće rezultate.

Iako konkretno dobijene statističke brojke ne odgovaraju projekciji iz teorije i dalje možemo ispitivati odnose između njih. Upoređivanjem vrednosti sa leve i desne strane jednačine (2) za dobijene statistike, možemo zaključiti da se one ne razlikuju previše i samim tim podržavaju hipotezu.

Drugi eksperiment koji sam izvršio je mnogo ekstremniji i baziran je na cugerima šahovskog kluba Beogradski Vodovod koji su se tradicionalno igrali skoro svakog ponedeljka i četvrtka. Arhiva turnira Večitog šaha [4] sadrži 258 tih turnira (uglavnom 15 kola po švajcarskom sistemu) što čini ogroman uzorak od 49639 odigranih partija. Kako FIDE rejting ovde nema puno smisla ja sam poodavno uveo poseban rejting za ove popularne cugere. Rejting sistem koji sam oformio po mnogim aspektima se razlikovao od FIDE rejtinga, a kao inspiracija poslužio je upravo Sonas-ov članak [3]. Skala je bila linearna gde je svaki rejting poen razlike označavao promil više preko 50%, a razlici od preko 500 rejting poena odgovarala je verovatnoća od svih 100%. Rejting je računat kao (linearni) performans na poslednjih 150 odigranih partija, pri čemu su, naravno, isključivane pobede koje smanjuju, odnosno porazi koji povećavaju taj performans. Ako igrač nije odigrao 150 partija, imao je performans na onome što je odigrao, ali na barem 75 partija, pri čemu su partije do 75. dopunjavane virtuelnim remijima protiv rejtinga 2000. Rejting liste su izlazile mesečno, a imale su veliku prednost što početni rejting nije bio bitan, jer igranje novih 10 turnira u potpunosti eliminiše stare rezultate.

Osnovna pretpostavka za ovaj eksperiment je ta da će ma kakav, iole logičan, rejting sistem, uspeti da pristojno diferencira igrače po jačini. Samim tim osnovna priroda ponašanja rejtinga pojaviće se kroz odgovarajuće statistike. Kao i u prvom primeru razvrstavao sam partije u klase od po 10 rejting poena i beležio statistike, a kompletan eksperiment zapisan je u tabeli na sledećoj strani.

Objasnimo najpre šta predstvaljaju kolone naše tabele. Prva kolona daje vrednost

koja predstavlja rejting klasu, odnosno situaciju kada je razlika u rejtingu oko 10

. Druga kolona daje broj obrađenih partija iz klase

, pri čemu su u obzir uzete samo partije gde su protivnici već stabilizovali rejting, odnosno odigrali bar 75 partija. Treća kolona daje procenat u slučaju da se rejting ponaša linearno, odnosno onako kako je predviđeno samim rejting sistemom. Četvrta kolona daje statistički procenat u klasi

. Peta kolona daje predviđanje procenta u klasi 2

po formuli (2) uz pretpostavku da se odnosi čuvaju, a šesta kolona daje stvarni statistički procenat u toj klasi. Poslednja kolona je apsolutna razlika prethodne dve kolone i predstavlja koliko je odstupanje od prognoze. Napomenimo još i to da su sve vrednosti u tablici zaokruživane na tri decimale.

Prilično odstupanje treće i četvrte kolone nam govori da je sam rejting sistem loše osmišljen, međutim male vrednosti u poslednjoj koloni pokazuju pravu prirodu rejtinga. Ovaj eksperiment me je u potpunosti ubedio da je očuvanje odnosa iz hipoteze jedan prirodni zakon koji mora da stoji iza svakog šahovskog rejtinga! Kako je izbor konstante C nebitan, najjednostavnije je uzeti utemeljeno C iz (4) da bi se izbegle neke dvosmislenosti i dodatna objašnjenja.

	uzorak	linear	f(10)		f(20)	diff
0	1574	0.5	0.5	0.5	0.5	0
1	1628	0.51	0.518	0.536	0.524	0.012
2	1690	0.52	0.524	0.548	0.562	0.014
3	1819	0.53	0.537	0.574	0.583	0.009
4	1714	0.54	0.562	0.623	0.6	0.023
5	1713	0.55	0.543	0.586	0.618	0.032
6	1739	0.56	0.583	0.661	0.645	0.016
7	1610	0.57	0.591	0.677	0.693	0.016
8	1769	0.58	0.6	0.692	0.702	0.01
9	1666	0.59	0.621	0.729	0.744	0.015
10	1630	0.6	0.618	0.724	0.755	0.031
11	1594	0.61	0.646	0.769	0.776	0.007
12	1556	0.62	0.645	0.767	0.779	0.012
13	1615	0.63	0.665	0.798	0.807	0.009
14	1476	0.64	0.693	0.836	0.817	0.019
15	1414	0.65	0.69	0.831	0.829	0.002
16	1373	0.66	0.702	0.847	0.855	0.008
17	1376	0.67	0.713	0.86	0.89	0.03
18	1338	0.68	0.744	0.894	0.844	0.05
19	1259	0.69	0.723	0.872	0.889	0.017
20	1232	0.7	0.755	0.905	0.914	0.009
21	1129	0.71	0.759	0.908	0.907	0.001
22	1113	0.72	0.776	0.923	0.949	0.026
23	1058	0.73	0.782	0.928	0.917	0.011
24	1040	0.74	0.779	0.925	0.961	0.036
25	902	0.75	0.81	0.948	0.948	0
26	930	0.76	0.807	0.946	0.963	0.017
27	854	0.77	0.827	0.958	0.995	0.037
28	712	0.78	0.817	0.952	0.977	0.025
29	709	0.79	0.823	0.956	0.958	0.002
30	667	0.8	0.829	0.959	0.985	0.026
31	662	0.81	0.855	0.972	0.966	0.006
32	645	0.82	0.855	0.972	0.977	0.005
33	611	0.83	0.849	0.97	0.985	0.015
34	541	0.84	0.89	0.985	1	0.015
35	497	0.85	0.882	0.983	1	0.017
36	458	0.86	0.844	0.967	1	0.033
37	403	0.87	0.895	0.986	0.941	0.045
38	382	0.88	0.889	0.985	1	0.015
39	338	0.89	0.898	0.987	1	0.013
40	324	0.9	0.914	0.991	1	0.009
41	320	0.91	0.897	0.987	1	0.013
42	275	0.92	0.907	0.99	1	0.01

U prethodnom tekstu smo statistički dokazali validnost formule (1), međutim ona je nepogodna za jednostavan račun. Za male vrednosti x možemo je aproksimirati koristeći Maclaurin-ov razvoj.

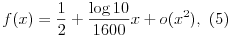koja jako dobro radi za |x|<100. Dakle, na intervalu |x|<100 funkcija f se ponaša linearno, a kako je 1600/log10 ~ 695, to možemo pisati

Prethodni račun dokazuje, među šahistima poznatu stvar, da svakom procentu preko 50% odgovara 7 (odnosno preciznije 6.95) rejting poena.

U daljem tekstu želimo da ispitamo koliki uticaj ima poslednje odigrana partija. Pretpostavimo zato da igrač ima zvanični rejting R0, ali je u međuvremenu napredovao (ili nazadovao) i sada vredi za R1. Ako on odigra jednu partiju, to će po FIDE pravilnicima [1] zaraditi razliku između ostvarenog i očekivanog rezultata pomnoženu sa K, gde je K razvojni koeficijent igrača. Tako dolazimo do očekivane zarade od K(f(R1-R0)-1/2). Sa druge strane zamislimo da je naš igrač odigrao N-1 partija snagom starog rejtinga, a onda odigrao partiju novom snagom. Performans koji je tako ostvario je ((N-1)R0+R1)/N, te se može reći da je u zaradi (R1-R0)/N. Poistovetimo li ove zarade, dobijamo jednačinu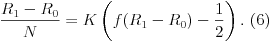

Štaviše, račun se sa jedne strane može uraditi i bez aproksimacije. Kako nam pažljiv račun daje f'''(0)=(1/8)(log C)^3<0, to se lako može pokazati da je f(x) < 1/2 + (log10)x/1600, za x>0, kao i simetrično f(x) > 1/2 + (log10)x/1600, za x<0. Ponovnim upoređivanjem kroz (6), možemo zaključiti da svakako važi

Poznato je da u FIDE za sada funkcionišu tri razvojna koeficijenta. K=25 imaju novi igrači dok ne odigraju barem 30 partija, K=10 igrači koji su nekad u karijeri premašili 2400 rejting poena, dok K=15 imaju svi ostali [1]. Na osnovu rezultata (7) možemo zaključiti da poslednje odigrana partija ima uticaj kao jedna od 695/K odigranih partija. Posmatrajmo sada novog igrača koji izlazi na rejting listu. Po FIDE pravilnicima kada neko odigra bar 9 partija protiv rejtingovanih igrača, on će kao početni rejting dobiti neku vrstu performansa za rezultat do 50%, a ako napravi preko 50% to će mu se na prosek protivnika dodati po 12.5 rejting poena za svakih osvojenih pola boda preko [1]. Posmatrajmo sada igrača koji se posle jednog turnira i 9 odigranih partija pojavio na rejting listi i samim tim dobio početni K=25. Sve dok bude imao taj koeficijent (prvih 30 partija) njegova poslednja partija vredeće po (7) kao jedna od 695/K ~ 28, iako je broj partija što ih je odigrao daleko manji od toga. Još bolju ilustraciju imamo kroz (8), gde vidimo da tih prvih 9 partija vrede kao da su igrane pod koeficijentom K > 695/9 ~ 77, a onda se to brutalno smanjuje više nego tri puta na 25. Još veća nepravda učinjena je igračima koji su na početku pravili preko 50% i zaradili samo 12.5 za svakih pola boda preko toga, jer su oni bonuse zarađivali po koeficijentu 25 iako su same te partije vredele za tri puta jači koeficijent.

Iz prethodno navedenog možemo zaključiti da je FIDE prilično loše rešila izlazak novog igrača na rejting listu, a to može imati dalekosežne posledice. Ukoliko igrač dobije prilično nerealan početni rejting, njemu je potrebno veoma mnogo vremena i odigranih partija da svoj rejting dovede na nivo za koji vredi, dok u međuvremenu utiče pozitivno ili negativno na rejting svojih protivnika.

Moj predlog je da pošto igrač zaradi početni rejting dobije i klizni koeficijent K=695/N, gde je N (hronološki) redni broj partije koju je odigrao protiv rejtingovanih igrača. Sudeći po (7) to je dobra aproksimacija, dok je sa druge strane zbog (8) to neki minimum koji treba postaviti. Klizni koeficijent bi trebalo da važi sve dok ne padne ispod vrednosti K0 koje smo namenili igračima sa stabilnim rejtingom, odnosno sve dok broj odigranih partija bude manji od 695/K0. Naravno dostizanje određenog rejtinga radi priznavanja titule valjalo bi računati samo pošto se desi prethodno navedeno, odnosno stabilizuje rejting.

Postoji mogućnost i radikalnijeg rešenja po kome svi igrači na početku dobijaju takozvani početni rejting, a onda sa njim ulaze u navedenu proceduru uz eventualno smanjivanje koeficijenta K za jako malo N (pre svega za N=1 i N=2). U tom slučaju zbog nepouzdanosti rejtinga igrača sa malim brojem partija trebalo bi modifikovati i koeficijent njegovog protivnika (pogotovo ako on ima stabilnih K0). Verujem da u slučaju da kad protivnici (po prethodnom) imaju koeficijente K i K1 < K, ovaj drugi (K1) treba pomnožiti sa K1/K.

Što se tiče najbolje vrednosti za K0, eksperimenti koje sam izvršio pokazali su da ako imamo dobro postavljen rejting sistem koeficijent K treba biti što manji. Po meni, osnovni problem je loše kreiran izlazak novog igrača na rejting listu i smatram da su sve vrednosti između 10 i 16 sasvim korektne. Međutim nikako ne mogu da preporučim uvođenje većih koeficijentata za igrače sa stabilnim rejtingom jer bi to u potpunosti upropastilo samu suštinu rejting sistema. Dodao bih i to da ne vidim bilo kakvu potrebu da postoji diskriminacija po tome da li je igrač nekada u karijeri prebacio rejting od 2400, te tako dobio drugačiji koeficijent.

Performans igrača je poslednjih godina jako bitna stvar jer se na osnovu njega osvajaju velemajstorske i intermajstorske norme. Međutim, način na koji se performans računa je prilično zabrinjavajući, a iznosi Ra+f^{-1}(p), gde je Ra prosečni rejting protivnika, dok je p procenat koji je igrač ostvario na turniru. Na turnirima se često dešava da neki protivnici imaju tako mali rejting da pobeda protiv njih zapravo umanjuje performans, te se zato zarad performansa za normu rejting najgorerejtingovanog igrača podiže da bi se eventualno stvar popravila. Moj predlog je da se performans definiše kao onaj rejting koji bi se sačuvao prilikom rejtingovanja dotičnog turnira. On se lako može iterativno sračunati, a ono što je dobro je što taj iterativni račun ne zavisi od razvojnog koeficijenta sa kojim se računa. Za ove račune ja ne bih koristio zaokruživanja iz tablice, već prave vrednosti funkcije f, naravno bez ikakvih rejting pragova od 400 rejting poena. U svakom slučaju pobeda nikako ne može da šteti, a popravljaju se i još neke stvari. Na primer, pretpostavimo da čovek osvoji 1.5 poen u dve partije sa prosekom protivnika od 2400, tada bi za FIDE račun performans bio 2591 (ili 2593 po tablicama). To bi bila i vrednost za moju računicu, ali samo ako oba protivnika imaju 2400. Međutim rejting nije linearan, što smo pokazali, te ako protivnici imaju 2300 i 2500 onda je performans 2605, a za protivnike od 2200 i 2600 performans je 2648! Ovakav iterativni račun će uvek konvergirati jednoj vrednosti, našem performansu, osim u slučaju svih pobeda ili svih poraza kada se performans ne može sračunati, što je i normalno.

Istina o šahovskom rejtingu

14.08.2010 / Andrejić, Vladica (2185)

Istina o šahovskom rejtingu

Vladica Andrejić

Univerzitet u Beogradu, Matematički fakultet, Srbija